緯度による日の出日の入り時間


緯度による日の出と日の入り時間の変化(2017／12／5)

　地球のように地軸の傾きがある惑星では、春分、秋分、夏至、冬至などの変化がある。
　地球の場合は地軸は約23.4度であり、緯度30度付近では夏至では春分の日(または秋分の日)
　よりも日の出は約一時間早く、日の入りは約1時間遅くなり、陽が出ている時間は春分の日より
　2時間以上長くなる。冬至と比べれば、4時間近くの差になる。
　日の出、日の入り時間は、太陽の位置を示す座標を赤道座標や地平座標と組み合わせて数式化
　し、地点の緯度とそのときの太陽の赤経から日の出、日の入り時刻、太陽の方位角などを求める。
　標準時線に対する経度差による時刻補正は容易だが、さらに以下の補正が必要になる。
　地球の公転軌道が楕円軌道であり完全な円軌道ではなく、地球の太陽に対する公転の角速度が
　一定でないことによる公転面に対する地軸の傾きの補正、大気による太陽光の屈折や太陽の大きさ
　によって生じる太陽の視差などによる補正である。

　ここでは公転面に対して地軸の傾きを持ち、自転する惑星のある緯度での夏至と春分の日の出、
　日の入りの時刻の変化を地平座標や赤道座標を使わず別の幾何学的なアプローチで求めてみる。
　但し、以下の条件での概略計算である。
　①惑星が恒星の回りを円軌道で回るものとする
　②恒星は十分離れており、恒星の視差は考慮しない。惑星への恒星の光は平行光線とみなす。
　③惑星の大気による恒星の光の屈折は考慮しない

　まず、半径1の球状で、公転面に対する地軸の傾きがψの惑星を仮定しよう。
　下記の図は、Z軸を地軸として、地球と同じ方向(北極点を上から見て反時計回り)に回転
　している惑星を示す。その惑星の緯度θの地点における春分の日と夏至の日の日没を考えてみる。
　
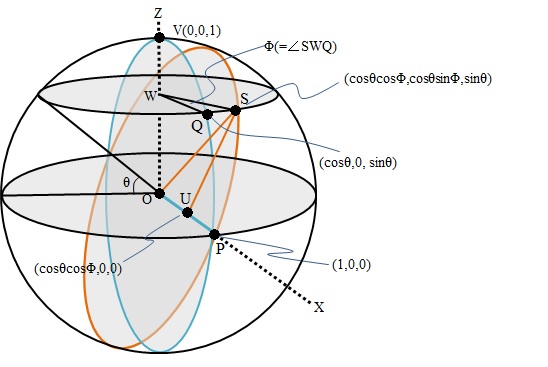
　春分の日没を迎えた惑星上の昼夜の境界を青い線(※1)で示す。
　このときの赤道上のP地点の座標を(1,0,0)、緯度θの地点をQとする。青い境界で囲まれた円と
　同一面上の直線は青い線で示す。
　（※1：恒星は十分遠方にあり、惑星に到達する恒星の光は平行光線とみなしてよいと仮定する）

　次に、P点が夏至の日没を迎えた時の惑星上の昼夜の境界線をブラウンの線で表す。
　ブラウンの境界線と緯度θの線が交差する地点をSとする。
　ここで、S点からx軸に垂直に引いた線分の交点をUとする。
　また、ブラウンの境界線で囲まれた円と同一面上にある線もブラウンの線で示す。
　(OPはブラウンの円の平面にも青い円の平面にも含まれるがここでは青い線で示す）
　夏至のときは、図に示すように地軸の傾きψのため、赤道上のP点が日没を迎えても、緯度θ
　のQ点はまだ日没を迎えず、Q点が日没を迎えるのはQ点が惑星の自転によってS点と同じ位置と
　重なった時点である。この春分の日没地点Qと夏至の日没地点Sの経度差Φ(∠SWQ＝Φ)が分かれば、
　惑星の自転の角速度を用いてQ点とS点の日没の時間差(＝日の出の時間差ともみなせる)を求める
　ことができる。従って、まず、この角度Φを求めることが主な目的になる。
　
　地軸の傾きψは、地軸方向のベクトルOV(0,0,1)とベクトルUSの成す角度であるから、
　OVのベクトルの大きさを|OV|(図から直ちに|OV|＝1となる）、USのベクトルの大きさを|US|として、
　ベクトルOZとUSの内積をOZ･USとすれば、内積の定義(※2)から下記の式が与えられる。
　OV･US＝|OV|･|US|cosψ＝|US|cosψ　・・・・(1)
　(※2：内積はそれぞれのベクトルの大きさと両ベクトルの成す角の余弦の積である)
　
　次にUの座標(図ではすでに(cosθcosΦ,0,0)で示している)を計算で確認しておく。
　Uはx軸上の点だから、一旦、(a,0,0)と置く。
　するとベクトルUSは点Uと点Sのx、y、zの各座標の差を取ればよいので、
　ベクトルUSは(cosθcosΦ－a,cosθsinΦ,sinθ)となる。
　ここでベクトルUSとx軸上のベクトルOP(1,0,0)の内積を考える。

　ベクトルUSとOPの内積は、両ベクトルの座標からも求めることができて、ベクトルのx座標同士、
　y座標同士、z座標同士の積の和を取ればよいので
　US・OP＝(cosθcosΦ－a,cosθsinΦ,sinθ)(1,0,0)＝(cosθcosΦ－a)・1＋cosθsinΦ・0＋sinθ・0
　＝cosθcosΦ－a

　一方、UはSからx軸に垂直に引いた線分の終点と仮定したから、ベクトルUSとx軸上のベクトルOPは
　直交する。直交するベクトルの内積は0であるから、US・OP＝0になる。
　従って、US・OP＝cosθcosΦ－a＝0となり、a＝cosθcosΦとなる。
　∴　座標Uは(cosθcosΦ,0,0)

　次に、USの大きさ|US|を求めておく。ベクトルUSは(cosθcosΦ－a,cosθsinΦ,sinθ)であったから、
　さきほど求めた結果、a＝cosθcosΦを使えば、ベクトルUSは
　US＝(0,cosθsinΦ,sinθ)・・・・(2)
　|US|²＝cos²θsin²Φ＋sin²θ
　|US|＝(cos²θsin²Φ＋sin²θ)^1/2　・・・・(3)

　OVとUSの内積は
　OV・US＝(0,0,1)・(0,cosθsinΦ,sinθ)＝0・0＋0・cosθsinΦ＋1・sinθ＝sinθ・・・・(4)
　一方、式(1)、(3)から
　OV･US＝|US|cosψ＝(cos²θsin²Φ＋sin²θ)^1/2・cosψ・・・・(5)

　従って、式(4)、(5)から、sinθ＝(cos²θsin²Φ＋sin²θ)^1/2・cosψ

　∴cosψ＝sinθ／(cos²θsin²Φ＋sin²θ)^1/2

　上式の 両辺を二乗して、cos²ψ＝sin²θ／(cos²θsin²Φ＋sin²θ)

　上の式から
　sin²Φ＝(sin²θ－sin²θcos²ψ)／(cos²θcos²ψ)＝sin²θ(1－cos²ψ)／(cosθcosψ)²＝sin²θsin²ψ／(cosθcosψ)²

　従って、求めるべきΦを含む式は以下のように非常にシンプルな式になる。
　sinΦ＝±sinθsinψ／(cosθcosψ)＝±tanθtanψ

　θは0～π／2、ψも0～π／2で想定すれば
　sinΦ＝tanθtanψ・・・・(6)（ここθは緯度、ψは地軸の傾き）

　従って、夏至では春分（または秋分）に対して惑星が下記の角度だけ
　自転する時間だけ日の入りは遅くなり、日の出は同じ時間だけ早くなる。
　Φ＝arcsin(tanθtanψ)・・・・(7)

　冬至では秋分（または春分）に対して惑星が上記の角度だけ
　自転する時間の分だけ日の出は遅くなり、日の入りは同じ時間だけ
　早くなる。


【地軸の傾きと緯度からの昼夜間時間の計算ツール】

このツールは式(7)をベースに地軸の傾きψを持つ球状の惑星の緯度θの地点の
夏至と冬至の昼夜間の日の出、日の入り及び昼夜間の時間差を計算する。
また、惑星が自転で15度回転する時間をその惑星の1時間とし、ツールのパラメータ
である地軸の傾きの初期値は現在の地球と同じ23.4度、緯度の初期値は30度としている。
地軸の傾きと緯度の初期値を任意に変えてシミュレートできる。
大気の屈折、恒星の視差は考えず、惑星の公転軌道は円軌道として計算している。
従って、このツールは大気がなく、恒星の視差を無視できるほど恒星から離れた
軌道を持つ惑星の計算に適する。

地軸の傾き度
緯度度



春分に対する夏至の日の出の時刻は下記だけ早く、日の入り時刻は下記だけ遅くなる。
　min
夏至に日が出ている時間は
　hr
冬至に日が出ている時間は
　hr

【参考】
恒星の視差(太陽の場合は16分(＝0.27度)）大気の屈折(地球の場合は34分(＝0.57度))は
このツールでは考慮してないので、実際に日が出ている時間に対して、ツールの計算時間は
短くなる。
地球の場合を例にとれば、緯度30度付近での夏至の昼間時間（日が出ている時間）については、
ツールの計算値は実際より10分程度短く、冬至の昼間時間の場合も実際より20分程度短くなる。
また、緯度が高くなるほどこの差が大きくなる。
一方、春分と夏至の実際の日の出時刻(または日の入り時刻)の変化はこのツールの計算値とよく
一致する。
春分と夏至との日の出時刻(または日の入り時刻)の差は東京(北緯35.65°)では、72分であるが、
ツールで求めた計算値も72分である。青森、神戸、那覇などの地点でもツールの計算値と一致する。


  
(ホームへ)
このページの無断転載、無断引用は禁じさせて頂きます。