古典力学で考えると
1500万度での陽子の運動エネルギー Eは、陽子間に働く反発の静電ポテンシャルエネルギーU の1／370 程度であり、
陽子同士を接触させるには完全なエネルギー不足であり核融合反応は起こり得ない。
1500万度の温度のエネルギーを持つ陽子同士が正面衝突した場合に陽子同士がどこまで接近できるか古典力学で
計算してみよう。正面衝突の場合は陽子同士の相対速度は2倍になるので、相対の運動エネルギーは4倍になる。
このときの陽子の運動エネルギーと等しい静電ポテンシャルエネルギーを持つ陽子の中心間距離をRとすると
Κe2／R ＝ 4×(3／2)kT
9.0×109×(1.6×10－19)2／R ＝ 4×3.11×10－16
∴R ＝ 1.86×10－13m
このRを古典力学的最小距離と呼ぶことにしよう。
この距離は陽子同士が接触するときの陽子の中心間距離＝2×10－15m に対して、約93倍も離れて
いることになる。
【2. 太陽中心での核融合反応とトンネル効果】
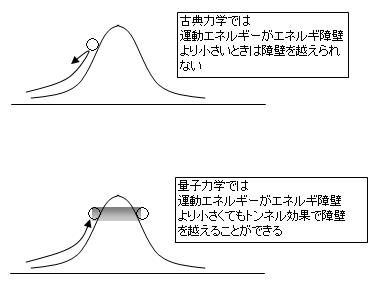
量子力学は、ポテンシャルエネルギー障壁を超えて粒子が存在する場合があることを予言した。(＝トンネル効果)
トンネル効果は江崎玲於奈博士によって、半導体研究中にPN接合ダイオードを用いて固体中で初めて実証され、
同博士は、1973年にノーベル物理学賞を受賞した。
古典力学ではありえない太陽の内部の核融合反応についても、このトンネル効果によって生じているといわれている。
ここでは陽子間に働く実際の静電ポテンシャル障壁ではなく、次に示す図のように矩形(長方形)のポテンシャル障壁に
簡略化し、トンネル効果による核融合発生確率の近似計算をしてみる。
次の図は陽子同士を接触させるために必要な静電ポテンシャルエネルギー U と同じ大きさの矩形のポテンシャル
エネルギー障壁に対して陽子が入射された場合を示したものである。
量子力学では波動関数で粒子の状態を記述するので、陽子が左側から入射され、反射及び浸透が起こる場合、
それぞれの状態に波動関数を与えて考える。
量子力学では、シュレディンガー方程式を解いて、陽子や電子といったミクロ粒子の波動関数を求めたり、エネルギーを
計算する。ここでは、入射する陽子のエネルギーが時間的に変化しない場合を想定してみる。
粒子のエネルギーEが時間的に変化せず一定の場合の一次元のシュレディンガー方程式は下記である。
E・ψ＝－h2／（8π2m)・(d2／dx2)ψ＋U・ψ (1)
(ここで E：粒子のエネルギー、ψ：粒子の波動関数、h：プランク定数、m：粒子の質量、U：ポテンシャルエネルギー)
上の図に従い、ポテンシャル障壁のないx＜0の領域とポテンシャル障壁のあるx＞0の領域の2つに分けて説明していく。
x＜0の領域について この領域ではポテンシャル障壁は存在しないので、ポテンシャルエネルギー U＝0 となる。 従ってシュレディンガー方程式は E・ψ＝－h2／（8π2m)・(d2／dx2)ψ (2) (尚、ここでは太陽中心部で1500万度の温度を持つ陽子同士が正面衝突する場合を考えている。衝突する相対速度は 2倍となるので、平均運動エネルギーは4倍ということで E＝4×(3／2)kT＝6kTを想定する。) 入射波の波動関数と反射波の波動関数を下記と置いてみる。 入射波：ψ1＝eiαx (α：定数) (3) 反射波：ψ2＝R・e－iαx (R：反射係数、α：定数) (4) 入射波と反射波については、x＜0の無限の領域のどこでも一様な波動関数として、虚数の入った平面波の波動関数を 適用している。 式(3)及び式(4)を式(2)のシュレディンガー方程式に適用して計算すると E・ψ1＝(αh)2／（8π2m)・ψ1 E・ψ2＝(αh)2／（8π2m)・ψ2 従って、次のように x＜0 の領域の入射波と反射波の陽子のエネルギー E 及び波動関数の係数αが求まる。 E＝(αh)2／（8π2m) (5) α＝(2π／h)・(2mE)1/2 (6)
x＞0の領域について 今回の目的である核融合の発生の確率を与える浸透波の波動関数を求めてみよう。 この領域では、陽子の波動関数は、ポテンシャル U ＝ 一定 の場に浸透していく。 太陽の中心部では、陽子の運動エネルギー E は、陽子同士が接触するまで接近するのに必要な静電 ポテンシャルエネルギー Uに比べてはるかに小さいので、ここでもU－E＞0を仮定する。 E も U も定数なので、式(1)のシュレディンガー方程式は次の形になる。 (U－E)・ψ＝h2／（8π2m)・(d2／dx2)ψ (7) 上のような方程式の一般解は、次の形を持つ。 ψ＝Ae－βx＋Beβx しかし、右辺の第二項は x が無限大では発散するため、物理的にはありえないので無視する。 従って、浸透波の波動関数としては ψ＝Ae－βx (8) となる。 式(8)を(7)に入れて計算すると上記の浸透波の波動関数の係数βが求められる。 (U－E)・ψ＝(βh)2／（8π2m)ψ ∴β＝(2π／h)・{2m(U－E)}1/2 (9) 量子力学では波動関数が規格化されているときはその関数を2乗したもの、すなわちψ2が粒子の存在の 確率密度関数となる。 ψ2＝A2・e－2βx (10) (注)確率密度関数ψ2では、区間 a ≦ x ≦ bでのψ2の面積＝その区間に陽子が存在する確率となる。 ここでは浸透時の核融合の発生確率を検討しているので、x＞0の全領域において陽子が必ず存在する 、すなわち存在確率＝1となるように規格化する必要がある。つまり、x＞0の領域で浸透波が下記を 満たすようにする。 ∫ψ2dx＝1 式(10)を用いると ∫∞0 A2・e－2βxdx＝A2／(2β)＝1 ∴A2＝2β 従って、陽子のポテンシャル U＝一定＞0の領域での規格化された陽子の確率密度関数は下記となる。 ψ2＝2β・e－2βx (ここでx＞0) (11) 次の図は、x ≧ 0 で U ＝一定のポテンシャル障壁に対する陽子の浸透波の確率密度関数を示したものである。 古典力学では陽子の運動エネルギー E と ポテンシャルエネルギーU で E＜U のときは反発されるので x＞0 の 領域には陽子は存在しないはずだが、量子力学で求めた確率密度関数は、x＞0の領域で減衰しながらも 0 ではなく、 浸透した陽子の存在を示している。 陽子同士が正面衝突して核融合を起こすためには、先にもとめた古典力学的最小距離 R から、さらに陽子同士が 接触する距離まで陽子が浸透する必要がある。 従って下記としたとき δ： 必要な浸透距離 R ： 古典力学的最小距離 (＝1.86×10－13m) r ： 陽子同士が接触したときの陽子の中心間距離 (＝2×10－15m) δ＝R－r (2008／05／21 記号で表現簡素化) (注) r は非常に小さいので計算上は無視して、δ＝Rとしてもよい。
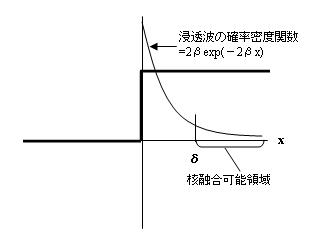実際の陽子がx＝δ(すなわち陽子同士が接触する距離) まで浸透した場合は、静電ポテンシャルよりもはるかに
強力な核力ポテンシャル(引力ポテンシャル)が作用してくるので陽子同士は融合を起こしてしまうだろう。
従って、 x≧δ の領域の確率密度関数 ψ2＝2β・e－2βx の面積は、核融合可能な確率にほぼ等しいと考えてみよう。
核融合の発生確率を γとすると
γ＝∫δ∞ ψ2dx
＝∫δ∞ 2β・e－2βxdx
＝ －〔e－2βx〕δ∞
＝e－2βδ
∴核融合の発生確率γ＝e－2βδ (ここでβ＝(2π／h)・{2m(U－E)}1/2)
さて、以下の数値で陽子同士が正面衝突する場合の核融合発生の確率を計算してみる。
U：陽子間静電ポテンシャルエネルギー ＝1.15×10－13J
E：陽子同士の正面衝突時の運動エネルギー(at 1500万K) ＝4×(3／2)kT＝1.24×10－15J
h：プランク定数 ＝6.625×10－34J・s
m：陽子の質量 ＝1.7×10－27kg
δ ：陽子の必要浸透距離 ＝1.86×10－13m
β＝(2π／h)・{2m(U－E)}1/2＝1.87×1014
従って、核融合の発生確率は
γ＝e－2βδ＝8.84×10－31
以上から、量子力学を用いた計算では、陽子と陽子が衝突したときに核融合が生じる確率 γ は
決して0 ではないという重要な計算結果が得られる。
ここで計算した核融合の確率は非常に低く、およそ1030回以上もの正面衝突で、ようやく核融合が
発生するという確率になる。しかし、次に示すように太陽中心部の陽子の膨大な衝突回数がその確率
の低さを補ってしまうのである。
太陽の中心部では、1m3あたりの陽子数は 約9×1031個といわれている。
古典力学的に接近できる陽子の中心間の最小距離Rを直径とする球として、陽子を考えた場合、単位
体積の陽子の個数と1500万度での陽子の平均速度から陽子の 平均自由行程を求め、一つの陽子が
他の陽子と衝突する回数を見積もると 2×1013回／秒にも及ぶ。
単純にこれらの数値の積をとっても、1m3内でも約9×1031個×2×1013回／秒＝1.8×1045回／秒のオーダー
の衝突になる。
正面衝突に近い衝突は限られてくるが、核融合を起こしている太陽中心部の体積を考えると膨大な数の
核融合が起こっていることになる。
(ホームへ)
ホームから入られた場合はこのページを閉じてください。